어그로 종자들(허세, ㅈㄹ, 관심병, 이렇게 세 분야의 거두가 한 분씩 활발하게 활동을 하심) 때문에 물갤이 어지러운 바, 이 몸이 물리와 조금이나마 관련이 있는 이야기를 해 보겠심.
양자역학 공부한 갤러들이라면 잘 알겠지만, 양자에는 2-state problem이 자주 등장한다. 왜냐? 우선, 우리가 closed form으로 답을 구할 수 있는 몇 안 되는 문제 중 하나이면서, 양자역학에서 배우는 여러 중요 개념들의 핵심을 이 간단한 문제를 통해 이해할 수 있기 때문. 대표적으로 energy gap이 어떻게 열리는지, 그리고 perturbation에 의해 고유값 및 고유벡터가 어떻게 바뀌는지 등이 있겠음. 구체적인 문제로는 자기장 내의 spin 1/2, BCS theory, unit cell 당 원자가 2개인 고체에서(ex: graphene) 원자 하나당 하나의 orbital만 고려할 때 tight-binding model, Brillouin zone boundary 근처에서 nearly free electron model 등이 정확히 2-state problem이 됨.
2-state problem에서 Hamiltonian은 물론 2x2 Hermitian matrix로 주어짐. 즉, 일반적으로 다음과 같은 형태.
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
...............(1)
(
과
는 실수)
를 대각화함으로써 문제를 푸는 것인데.... 2x2 행렬을 대각화하는 게 뭐가 대수냐? Characteristic equation 세워서 근의 공식으로 풀면 되는데? 물론 맞는 말이지만, 2x2행렬의 요소가 숫자가 아니라 문자인 경우, 이 방식으로 고유값과 고유벡터를 구하는 것은 상당히 귀찮은 일이며, 이렇게 자주 나오는 문제는 매번 다시 푸는 것보다 그냥 답을 외워버리면 두고두고 편리하다. 답을 외운다고, 복잡한 식을 무작정 외우자는 것이 아니라, 왜 그런 결과가 나오는지에 대한 이해가 있으면 쉽게 머릿속에 들어옴. 따라서 그 중간 과정에 대해 이야기해 보겠음.
임의의 2x2 Hermitian matrix에는 네 개의 독립적인 실수 성분이 존재하는데, 위에서 정의한
를 기준으로
,
,
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
,
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
임. 그에 따라
를 다음과 같이 표현할 수 있음.
%20%5C%5C%20+%20%5C%5C%20%5C%5Cfrac%7B%5C%5Cvarepsilon_%7B1%7D-%5C%5Cvarepsilon_%7B2%7D%7D%7B2%7D%20%5C%5Cleft(%5C%5Cbegin%7Barray%7D%7Bcc%7D1&0%5C%5C%5C%5C0&-1%5C%5Cend%7Barray%7D%5C%5Cright)%20%5C%5C%5C%5C%20%5C%5C%5C%5C%5C%5Cindent%5C%5Cindent+%20%5C%5C%20%5C%5Ctextmd%7BRe%7D(V)%20%5C%5Cleft(%5C%5Cbegin%7Barray%7D%7Bcc%7D0&1%5C%5C%5C%5C1&0%5C%5Cend%7Barray%7D%5C%5Cright)%20%5C%5C%20+%20%5C%5C%20%5C%5Ctextmd%7BIm%7D(V)%20%5C%5Cleft(%5C%5Cbegin%7Barray%7D%7Bcc%7D0&-i%5C%5C%5C%5Ci&0%5C%5Cend%7Barray%7D%5C%5Cright) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.......................(2)
이 선형 결합에 등장하는 네 개의 Hermitian matrix들은 각각 고유의 이름이 있는데, 우선 다음과 같은 identity matrix.
나머지 셋은 Pauli matrix라고 하여 다음과 같이 정의됨.
이들 Pauli matrices는 다음과 같은 성질을 가짐을 보일 수 있음. (계산해 보면 간단히 나옴.)
,
(x->y->z->x로 cyclic permutation해도 성립. 여기서 i는 허수 i를 의미)
또한, 두 번째 성질에 의해 다음이 성립.
여기서 재미있는 성질을 이끌어낼 수 있는데, 바로 다음.
여기서 벡터
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
의 각 성분은 실수이며, 벡터
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
의 각 성분은 Pauli matrix임. 이때, 아래와 같이 고유값 방정식을 써 보면
%5E%7B2%7D=%7C%5C%5Cvec%7Ba%7D%7C%5E%7B2%7D%20%5C%5C,I "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
라는 조건이
의 고유값에 제약을 가함을 알 수 있음.
위의 제약조건에 따르면,
가 가지는 두 고유값은 둘 다
이거나, 둘 다
이거나, 또는 하나는
이고 다른 하나는
이어야 함. 여기서 앞의 두 경우는 불가능. 왜냐하면, 두 고유값이 같다는 것은
이
에 비례함을 의미하는데,
의 trace(두 대각 성분의 합)는 0이 아닌 반면에,
는 trace는 0이기 때문. (Pauli matrix들은 trace가 모두 0임.)
따라서,
의 고유값은
.
이제 식 (2)로 주어지는
의 표현식에서
에 비례하는 부분을 제외하면 다음과 같이 대응시킬 수 있음.
,%5C%5Cquad%20a_%7By%7D%20=%20%5C%5Ctextmd%7BIm%7D(V),%5C%5Cquad%20a_%7Bz%7D%20=%20%5C%5Cfrac%7B%5C%5Cvarepsilon_%7B1%7D-%5C%5Cvarepsilon_%7B2%7D%7D%7B2%7D "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.............(3)
따라서 이 경우
의 고유값은 다음과 같음.
한편, 식 (2)에서
에 비례하는 부분이 고유값에 하는 일은 단지
앞의 계수만큼을 더해 주는 것 뿐이므로,
의 고유값은 다음과 같이 주어짐.
%5E%7B2%7D+%7CV%7C%5E%7B2%7D%7D "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
....................(4)
그렇다면 고유벡터는 어떻게 될까? 어떤 행렬에 상수를 곱해도 그 고유벡터는 변하지 않으므로, 우리는 임의의 3차원 벡터
대신, 임의의 3차원 단위 벡터
를 고려하면 됨. 또한, identity에 비례하는 행렬을 더해도 고유벡터가 바뀌지 않으므로, 식 (2)에서
에 비례하는 항은 고유벡터에 영향을 주지 않음.
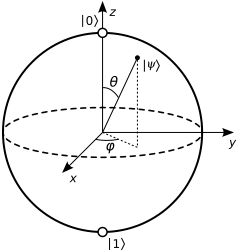
이제 임의의 3차원 단위 벡터를 다음과 같이 매개변수화하는 것이 가능.
즉, 구면 좌표계를 사용한 것과 같음. (
,
) 식 (3)과 같이 대응시킬 경우,
을 매개변수화한 위 식에 등장하는 두 각도 변수는 다음에 해당.
이때,
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
위 행렬의 고유값은 앞서의 결과로부터
이 됨을 알 수 있고, 그 고유벡터를 구해 보겠음. 고유값 1에 대한 고유벡터
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
는 다음을 만족.
따라서 고유값 1에 대한 규격화된 고유벡터를 다음과 같이 쓸 수 있음.
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
............(5-1)
비슷한 계산 과정을 고유값 -1에 대해 수행해 보겠음.
그에 따라 고유값 -1에 대한 규격화된 고유벡터를 다음과 같이 쓸 수 있음.
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
..........(5-2)
이제까지의 결과를 종합하면, 일단 우리는 다음과 같은 2-state problem의 Hamiltonian에서 시작하였음.
...............(1)
이것을 identity와 Pauli matrix들의 선형결합으로 나타내면 다음과 같음.
%20I%20+%20%5C%5Cleft(%20%5C%5Cfrac%7B%5C%5Cvarepsilon_%7B1%7D-%5C%5Cvarepsilon_%7B2%7D%7D%7B2%7D%20%5C%5Cright%20)%5C%5Csigma_%7Bz%7D%20+%20%5C%5C%20%5C%5Ctextmd%7BRe%7D(V)%20%5C%5C,%5C%5Csigma_%7Bx%7D+%20%5C%5C%20%5C%5Ctextmd%7BIm%7D(V)%20%5C%5C,%5C%5Csigma_%7By%7D "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
............. (2')
의 고유값이
라는 것으로부터
의 고유값이 다음과 같음을 유추할 수 있음.
....................(4)
또한 이 두 고유값에 대응되는 규격화된 고유벡터들은 각각 다음과 같이 쓸 수 있음.
,%20%5C%5Cquad%7C%5C%5Cpsi_%7B-%7D%5C%5Crangle%20=%20%5C%5Cleft(%5C%5Cbegin%7Barray%7D%7Bc%7D%5C%5Cdisplaystyle%7B-%5C%5Csin%5C%5Cfrac%7B%5C%5Ctheta%7D%7B2%7D%7D%5C%5C%5C%5C%20%5C%5C%5C%5C%5C%5Cdisplaystyle%7B%5C%5Ccos%5C%5Cfrac%7B%5C%5Ctheta%7D%7B2%7D%7De%5E%7Bi%5C%5Cphi%7D%5C%5Cend%7Barray%7D%20%5C%5Cright%20) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.................. (5-1), (5-2)
여기서 각도 변수들은 다음과 같이 정의됨.
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
간단히 말해 3차원 실수 벡터
,%5C%5Ctextmd%7BIm%7D(V),%5C%5Cfrac%7B%5C%5Cvarepsilon_%7B1%7D-%5C%5Cvarepsilon_%7B2%7D%7D%7B2%7D%20%5C%5Cright%20) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
를 구면좌표계에서 나타냈을 때의
,
에 해당.
마지막으로,
에 나오는
와
을 굳이
,
,
로 표현하려면, 다음 관계식을 이용하면 됨.
제곱근 앞의 부호가 (+)와 (-)가 둘 다 가능하지 않느냐고 물을 수 있겠으나, 이 경우는
라는 조건 때문에 언제나 (+)로 정해짐.
댓글 영역
획득법
① NFT 발행
작성한 게시물을 NFT로 발행하면 일주일 동안 사용할 수 있습니다. (최초 1회)
② NFT 구매
다른 이용자의 NFT를 구매하면 한 달 동안 사용할 수 있습니다. (구매 시마다 갱신)
사용법
디시콘에서지갑연결시 바로 사용 가능합니다.